使用Python对二维数据进行插值

背景

因为一个程序中需要保存的数据太大，所以需要进行采样，保存稀疏网格上的值。在计算完成后，返回原来密集网格上的值。本来使用的是Scipy.interpolate.griddate，效率十分低。

后来查阅相关文档，发现Scipy提供了两种插值模式，分别对应矩形网格和非结构网格，前者效率更高。而对于我的问题，结构网格完全适用。

文档

class scipy.interpolate.interp2d(x, y, z, kind=’linear’, copy=True, bounds_error=False, fill_value=nan)
Interpolate over a 2-D grid.

x, y and z are arrays of values used to approximate some function f: z = f(x, y). This class returns a function whose call method uses spline interpolation to find the value of new points.

If x and y represent a regular grid, consider using RectBivariateSpline.

Parameters :

  • x, y : array_like

    Arrays defining the data point coordinates.

    If the points lie on a regular grid, x can specify the column coordinates and y the row coordinates, for example:

    x = [0,1,2]; y = [0,3]; z = [[1,2,3], [4,5,6]]

    Otherwise, x and y must specify the full coordinates for each point, for example:

    x = [0,1,2,0,1,2]; y = [0,0,0,3,3,3]; z = [1,2,3,4,5,6]

    If x and y are multi-dimensional, they are flattened before use.

  • z : array_like

    The values of the function to interpolate at the data points. If z is a multi-dimensional array, it is flattened before use. The length of a flattened z array is either len(x)*len(y) if x and y specify the column and row coordinates or len(z) == len(x) == len(y) if x and y specify coordinates for each point.

  • kind : {‘linear’, ‘cubic’, ‘quintic’}, optional

    The kind of spline interpolation to use. Default is ‘linear’.

  • copy : bool, optional

    If True, the class makes internal copies of x, y and z. If False, references may be used. The default is to copy.

  • bounds_error : bool, optional

    If True, when interpolated values are requested outside of the domain of the input data (x,y), a ValueError is raised. If False, then fill_value is used.

  • fill_value : number, optional

    If provided, the value to use for points outside of the interpolation domain. If omitted (None), values outside the domain are extrapolated.

例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp2d

def func(x, y):
    return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2

# @profile
def interp1(x, y, values):
    # regard as rectangular grid
    f1 = interp2d(x, y, values, kind='cubic')
    return f1

def interp2(xx, yy, values):
    # regard as unstructured grid
    x_flat, y_flat, z_flat = map(np.ravel, [xx, yy, values])
    f2 = interp2d(x_flat, y_flat, z_flat, kind='cubic')
    return f2


if __name__ == "__main__":
    # Data point coordinates
    x = np.linspace(0, 1, 20)
    y = np.linspace(0, 1, 30)
    xx, yy = np.meshgrid(x, y)
    values = func(xx, yy)
    
    f1 = interp1(x, y, values)
    f2 = interp2(xx, yy, values)
    
    # Points which to interpolate data
    x_flat = np.linspace(0, 1, 100)
    y_flat = np.linspace(0, 1, 200)
    
    z1 = f1(x_flat, y_flat)
    z2 = f2(x_flat, y_flat)
    plt.figure()
    plt.imshow(values, extent=(0, 1, 0, 1))
    plt.title("Origin")
    plt.figure()
    plt.subplot(211)
    plt.imshow(z1, extent=(0, 1, 0, 1))
    plt.title("rectangular grid")
    plt.subplot(212)
    plt.imshow(z2, extent=(0, 1, 0, 1))
    plt.title("unstructured grid")
    plt.show()

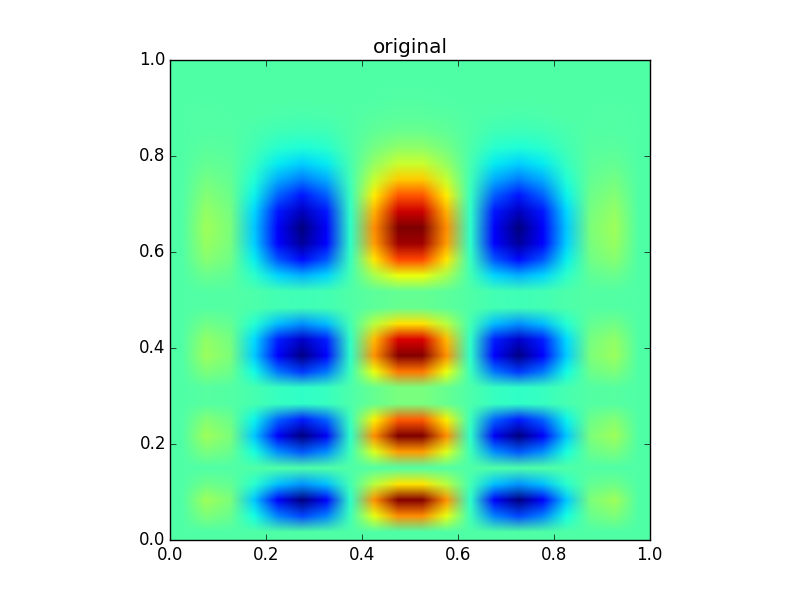
original

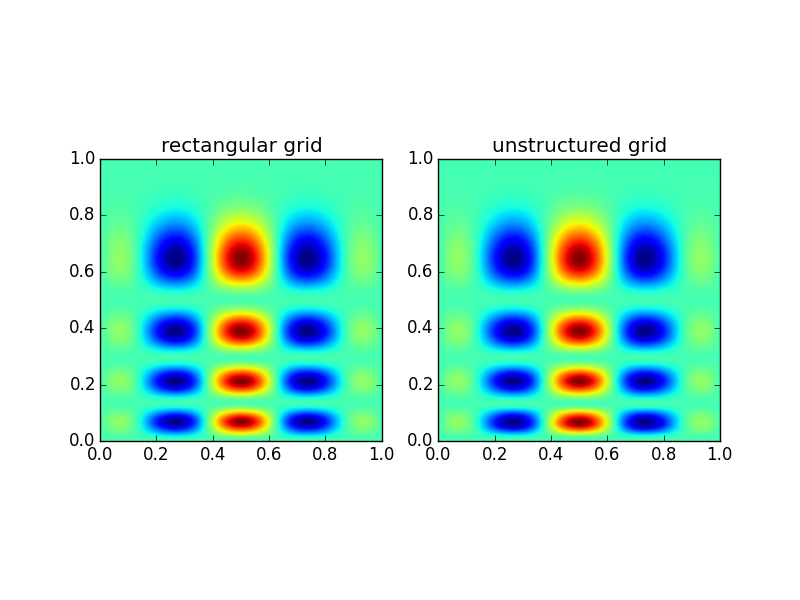
interp

计算时间对比：

  • 矩形网格（interp1）：0.000456 s
  • 非结构网格（interp2）：0.098047 s

可见差别非常大，当原始网格更多的时候，对比就越明显。